In this article, we discuss a class of transactions that change the states of multiple shards, i.e., cross-shard transactions. For example, user A transfers its token in shard X to user B’s address in shard Y, and thus the balance of user A in shard X is reduced, and the balance of user B in shard Y is increased.
One key property we would like to maintain for a transaction is atomicity — all the operations must either succeed with a new state or fail without changing the state in a transaction. In the balance transfer case, this means that either all user balances are unchanged (failed case) or sender balance and receiver balance are updated accordingly. In an in-shard transaction that only changes the state in a single shard, the operations are synchronously executed in one block and thus atomicity can be guaranteed. For a cross-shard transaction, to guarantee atomicity is much more difficult:
- The operations are asynchronously executed in different blocks in different shards. How to ensure all the operations are executed eventually in different shards, i.e., incentives of executing the operations, is challenging.
- To ensure atomicity, the operations will be executed in the order in different blocks that belong to different shards. How to ensure the temporal order (happens-before) relationship of the operations is difficult.
- If an attacker tries to revert a block that contains an operation of the transaction, will the rest operations of the transaction be canceled or reverted? If not canceled, then we have a security problem and the atomicity cannot be guaranteed. For example, if the withdraw operation of a balance transfer is reverted, while the deposit operation still exists, then the total supply of the token can be artificially increased.
In addition, by increasing more shards in the network, the cross-shard transactions will dominate all transactions, and thus the scalability of cross-shard transactions becomes an issue. For example, suppose a user randomly transfers some tokens to another user’s address in a random shard, the probability of the transaction being a cross-shard transaction is (N — 1) / N. This means that if there are two shards, 50% of transactions will be cross-shard, and if we have 10 shards, 90% of transactions will be cross-shard. How to scale the cross-shard transactions is a critical issue in blockchain sharding.
The probability of Cross-Shard Tx
Another common issue in sharding is the hot-shard problem: if a lot of cross-shard transactions are sent to a target shard, the target shard would rate limit the processing of the cross-shard transactions to prevent its BPs from being overwhelmed.
In the following, we will explain the details of how QuarkChain’s Boson consensus algorithm achieves atomicity, security, and scalability of cross-shard transactions.
Anatomy of a Blockchain Transaction
We consider the following cross-shard transactions:
- Balance transfer: User address A in shard X transfers its token to user address B in shard Y;
- Smart contract transaction: User address A in shard X calls another smart contract address B in shard Y.
Note that in Ethereum, the difference between these two transactions is that whether the code field of address B is empty (user address) or not (smart contract address).
In the context of Ethereum-like network, the transaction consists of the following operations:
- ( Balance withdraw ): The operation withdraws the tokens from the balance of address A. The number of tokens equal to the amount to transfer + the reserved transaction fee (gasPrice * startGas). This operation happens in shard X
- ( Execution ): For balance transfer, the execution increases the balance of user B, or for smart contract transaction, the execution runs the code of the smart contract C. This operation happens on shard Y.
- ( Refund ): After running the transfer/smart-contract-call, the actual transaction fee is calculated, and the remaining transaction fee (reserved — actual) is refunded to user A. The result of the operation will be written to the ledger of shard X.
Illustration of a Cross-Shard TX
One good property of the blockchain transaction is that as long as the operation 1 is succeeded, the operations 2 and 3 will not revert operation 1, i.e., even the smart contract call in operation 2 fails, we will continue to refund the user’s transaction fee instead of reverting operation 1. This transaction model could make atomicity much easier without resorting to the traditional roll-back mechanism as in the transaction of a centralized database.
Moreover, the model can be applied to other transaction models such as EOS, where the withdraw operation will withdraw other resources (CPU, NET) rather than EOS token.
Simplification of Cross-Shard Transaction
The first step of optimizing cross-shard transaction in QuarkChain is to simplify the refund step. The idea is based on the QuarkChain feature that a user has an address in every shard, and thus the refund could be done in the target shard rather than the source shard. The list of operations becomes:
- ( Balance withdraw ): The operation withdraws the tokens from the balance of user A. The number of tokens equal to the amount to transfer + the reserved transaction fee (gasPrice * startGas). This operation happens in shard X.
- ( Execution/Refund ): For balance transfer, the execution increases the balance of user B, or for smart contract transaction, the execution runs the code of the smart contract C. After running the transfer/smart-contract-call, the actual transaction fee is calculated, and the remaining transaction fee (reserved — actual) is refunded to user A’s address in shard Y. This operation happens in shard Y.
Since the amount of the refund is generally a small amount (zero for most balance transfer transactions), a user could move the balance back to its primary shard as needed if the balance is accumulated as a large value. QuarkChain’s smart wallet will help a user to collect all these small funds back to the user’s primary shard in a single click.
Simplification of the Cross-Shard Tx
Order of Cross-Shard Transaction Operations
The next step is to ensure the happens-before relationship between Operation 1 (Withdraw) and Operation 2 (Execute/Refund). QuarkChain ensures the happens-before relationship by using rootchain as a clock:
- A sharded block has two hash pointers: one links to the previous sharded block in the shard and another one links to the latest root block. Note that the height of the rootchain included in the sharded blocks must be non-decreasing.
- To perform Operation 2 (Execution/Refund) of a transaction, the corresponding sharded block (block M + 2) must include the root block height greater than or equal to the root block with height (L + 1), which contains the header of the sharded block that performs operation 1 (N + 1).
As a result, we could guarantee that Operation 2 (Execution/Refund) always comes after Operation 1 (Withdraw).
Double-Spending Attack on Cross-Shard Transactions
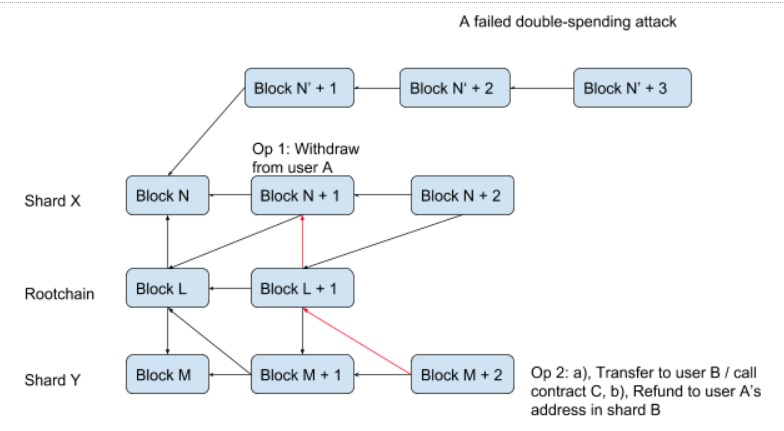
A critical attack in cross-shard transactions is to revert operation 1 (Withdraw) after operation 2 (Execution/Refund) is executed, and if operation 2 is not properly handled (e.g., canceled), it will cause catastrophic consequences. In the balance transfer context, this means additional tokens are created, i.e., the total supply assumption of the token is broken. Thanks to Boson consensus run by QuarkChain, the attacker will fail to perform such an attack if it tries to revert the block contains operation 1 (e.g., block N + 1) by creating a longer shard fork (e.g., blocks N’+1 to N’+3).
A Failed Double-Spending Attack
To revert the withdraw operation of the cross-shard transaction, the attacker must revert the root block (e.g., block L + 1) that contains the header/hash of the block containing Operation 1 (Withdraw) (e.g., block N + 1) by creating a long rootchain fork (e.g., Block L’ + 1, Block L’ + 2). Since rootchain describes the canonical chains of all shards, all shards will automatically switch to the shard forks described by the rootchain (recall rootchain-first fork choice rule). This means that the following Operation 2 (Execute/Refund) will be automatically reversed as a result of the attack (e.g., block M + 2 becomes a stale as it points to a stale root block (e.g., block L + 1)).
A Successful Double-Spending Attack
Relationship with DAG
With the two hash pointers of each sharded block, QuarkChain block structure is essentially a directed acyclic graph (DAG), and Operation 1 precedes Operation 2 in the order. However, compared to other DAGs, QuarkChain is well-structured in the following aspects::
- Given two DAGs of QuarkChain, we could easily determine which DAG should be chosen by using root-chain first fork rule (See Part 4). In addition, the attack vector and security level of QuarkChain are well defined (e.g., 51% hash power of the rootchain to perform double-spending attack if rootchain runs PoW).
- With the sharding structure of the DAG, we could optimize the system performance by using multi-threading or clustering, where the transactions/storages of the blocks are processed by different threads or processes.
- In addition, we define the neighborhood of a shard, where a shard could only directly send a cross-shard transaction to its neighbor directly, and multiple-hop routing is required if two shards are not neighbor. This means that the cost of broadcasting cross-shard transactions of a sharded block to its neighbor is O(NM) where N is the number of shards and M is the maximum number of neighbors.
Hot-Shard Issue and Throttling
If multiple shards send a lot of cross-shard transactions simultaneously, the target shard may be overwhelmed by the transactions. For example, if a hot ICO happens in one shard, the users from all shards try to join the ICO, and the shard hosts the ICO may have to process a lot of cross-shard transactions in a short time. Since the throughput of one shard is limited, how to process these transactions and prevent the shard being crashed is a problem. We refer to this as a hot-shard issue. To address this issue, the cross-shard transactions will be processed in the shard in a round-robin way:
- When creating a sharded block, a BP recovers a list of pending sharded blocks whose cross-shard transactions are not processed by the previous sharded block.
- If a new root block is included in the sharded block, the headers of the neighbors are appended to the list. Since multiple sharded block headers are added, the headers from different shards will be appended in a round-robin way.
- Each block has cross-shard transaction gas limit, and the BP pops the headers from the list. For each header, the BP looks up and processes the cross-shard transactions included in the corresponding block. The process repeats until the cross-shard transaction gas limit is exhausted.
Following this way, we could make sure each block does not process the transactions that exceed its cross-shard limit. This is similar to CPU task scheduling, where a CPU allocates a scheduling quantum to each task, and switch to the next task if the quantum is expired.
Scalability
Let us assume the extreme case, where all shards are busy with cross-shard transactions. This means that the pending queues of unprocessed cross-shard transactions are full for all shards. Therefore, all the cross-shard transaction gas limit are exhausted, and the cross-shard transaction throughput is
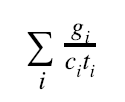
where g_i is the cross-shard transaction gas limit of shard i, c_i is the average transaction gas, and t_i is the block interval. Consider a homogeneous sharding case where each shard runs the same consensus with g_i, c_i, t_i being the same for all shards, the cross-shard transaction capacity increases linearly as the number of shards increases.
Summary
In this article, we presented the cross-shard transaction details of QuarkChain. We discussed how QuarkChain achieves atomicity, security, scalability, and addresses the hot-shard problem. In the next article, we will discuss more details about the implementation of QuarkChain to enable high-performance nodes, via clustering.